Just because you are using a true RMS multimeter does not automatically mean you should always trust the readings of your measurements. In fact, most true RMS multimeters can only offer reliable readings under certain conditions. In this post, I will examine some of the pitfalls in RMS voltage measurements and show you some concrete examples on how RMS readings can sometimes be misleading.
True RMS multimeters are noticeably more expensive than their non-RMS counterparts (i.e. average rectified multimeter). But before jumping onto the true RMS bandwagon, we need to fully understand some of the common limitations most true RMS meters have. As you can see later, whether or not an RMS meter gives accurate measurements is dependent on the task at hand.
Generally speaking, the measurement accuracy of a RMS multimeter is highly dependent upon the followings:
- Voltage waveform: Most middle-range RMS multimeters will only give accurate readings when the AC waveform to be measured is symmetrical. As we will see later, asymmetrical waveforms can attribute to significant reading deviations from the true measurements.
- DC Component: Unless the meter is advertised as capable of RMS measurement in both AC and DC range, chances are the multimeter will not be able to measure correctly when the waveform has a DC component. Even if the meter in use can handle AC + DC RMS readings, it would still be more accurate in general to use the following equation to determine the true RMS value of the measurement:
- Signal frequency The frequency range of the signal to be measured tends to have a larger impact on RMS multimeters than none-RMS multimeters. Typically, RMS meters can only measure accurately when the waveform frequency is below a couple of kHz.
Crest factor of the waveform also affects the measurement accuracy. A typical RMS meter can only obtain accurate readings when crest factor is below 3 to 4.
\[V_{RMS}=\sqrt{V_{AC_{RMS}}^2 + V_{DC}^2}\]
Now, let us take a look at a couple of examples to see how true RMS meters perform in the real world.
TRIAC Waveform
Typically, averaging multimeter is tuned specifically to measure sinusoidal voltages with frequency up to a few hundred Hertz (e.g. power main). As the waveform deviates from sinusoidal the measurement accuracy drops. For instance, the following oscilloscope image (RIGOL DS1052E) shows a typical waveform of a DIAC-triggered TRIAC dimmer circuit.
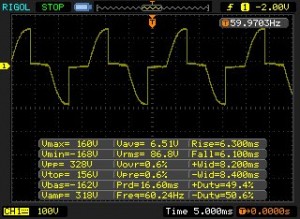
When measured using a true RMS meter (BK 2709B) the voltage reading was 86.8V which is dead on compared to the oscilloscope measurement. When using a none-RMS meter (Craftsman 82339)the voltage reading changed to 65.6, which is almost 25% off the accurate measurement.
Generally speaking, true RMS meters are well suited for electrician type of work. And true RMS meters have a high accuracy when the waveform to be measured is symmetrical.
Square Wave
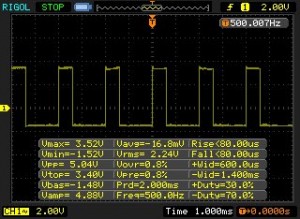
When measuring square wave, the situation is no longer as simple as before. Depending on the frequency and duty cycle, the RMS measurements can vary drastically. In general, the measurement error increases as the waveform frequency increases and the waveform duty cycle deviates further from 50%.
The following table shows the readings of squarewave voltages of different duty cycles from a true RMS meter (BK Precision 2709B), an averaging meter (Craftsman 82339) and an oscilloscope (Rigol DS1052E).
Column headers:
- Duty Cycle: the duty cycle of the square wave
- Frequency: the frequency of the square wave (Hertz)
- RMS (V): the measurement from a RMS meter.
- RMS Err %: the RMS measurement error compared with the theoretical RMS value
- AVG (V): the measurement from an averaging meter.
- AVG Err %: averaging measurement error compared with the theoretical RMS value
- RMS (osc. V): the measurement from a DSO.
- RMS (osc) Err %: Oscilloscope RMS measurement error compared with the theoretical RMS value.
- Vmax: the maximum voltage reading of the waveform (from DSO)
- Vmin: the minimum voltage reading of the waveform (from DSO)
- Vrms(calc): theoretical RMS value calculated from Vmax, Vmin and the duty cycle
| Duty Cycle | Frequency (Hz) | RMS (V) | RMS Err % | AVG (V) | Avg Err % | RMS (osc. V) | RMS (osc) Err % | Vmax | Vmin | Vrms (calc) |
| 0.1 | 50 | 1.441 | 3.25% | 1.13 | 24.13% | 1.47 | 1.30% | 4.40 | -0.56 | 1.49 |
| 500 | 1.409 | 5.40% | 1.16 | 22.12% | 1.47 | 1.30% | ||||
| 5000 | 0.838 | 43.73% | 1.31 | 12.04% | 1.35 | 9.36% | ||||
| 10000 | 0.596 | 59.98% | 1.47 | 1.30% | 1.45 | 2.64% | ||||
| 0.2 | 50 | 1.925 | 6.01% | 1.92 | 6.25% | 1.97 | 3.81% | 4.08 | -1.04 | 2.05 |
| 500 | 1.906 | 6.94% | 1.96 | 4.30% | 1.97 | 3.81% | ||||
| 5000 | 1.571 | 23.29% | 2.29 | 11.81% | 1.97 | 3.81% | ||||
| 10000 | 1.062 | 48.15% | 2.41 | 17.67% | 1.89 | 7.72% | ||||
| 0.3 | 50 | 2.212 | 4.23% | 2.41 | 4.35% | 2.25 | 2.58% | 3.52 | -1.52 | 2.31 |
| 500 | 2.194 | 5.01% | 2.46 | 6.51% | 2.25 | 2.58% | ||||
| 5000 | 1.850 | 19.90% | 2.70 | 16.90% | 2.22 | 3.88% | ||||
| 10000 | 1.394 | 39.64% | 2.94 | 27.29% | 2.17 | 6.05% | ||||
| 0.4 | 50 | 2.371 | 5.49% | 2.63 | 4.83% | 2.40 | 4.33% | 3.12 | -2.00 | 2.51 |
| 500 | 2.351 | 6.29% | 2.70 | 7.62% | 2.39 | 4.73% | ||||
| 5000 | 2.079 | 17.13% | 3.01 | 19.98% | 2.39 | 4.73% | ||||
| 10000 | 1.615 | 35.62% | 3.26 | 29.95% | 2.33 | 7.12% | ||||
| 0.5 | 50 | 2.423 | 3.86% | 2.63 | 4.35% | 2.43 | 3.58% | 2.56 | -2.48 | 2.52 |
| 500 | 2.402 | 4.69% | 2.71 | 7.53% | 2.44 | 3.19% | ||||
| 5000 | 2.133 | 15.37% | 3.03 | 20.22% | 2.44 | 3.19% | ||||
| 10000 | 1.782 | 29.29% | 3.39 | 34.51% | 2.45 | 2.79% | ||||
| 0.6 | 50 | 2.374 | 5.36% | 2.42 | 3.53% | 2.40 | 4.32% | 2.08 | -3.04 | 2.51 |
| 500 | 2.354 | 6.16% | 2.51 | 0.06% | 2.40 | 4.32% | ||||
| 5000 | 2.079 | 17.12% | 2.82 | 12.42% | 2.41 | 3.93% | ||||
| 10000 | 1.741 | 30.60% | 3.24 | 29.16% | 2.43 | 3.13% | ||||
| 0.7 | 50 | 2.219 | 7.00% | 2.04 | 14.50% | 2.25 | 5.70% | 1.68 | -3.52 | 2.39 |
| 500 | 2.200 | 7.79% | 2.12 | 11.15% | 2.25 | 5.70% | ||||
| 5000 | 1.949 | 18.31% | 2.53 | 6.04% | 2.29 | 4.02% | ||||
| 10000 | 1.615 | 32.31% | 2.96 | 24.06% | 2.35 | 1.51% | ||||
| 0.8 | 50 | 1.933 | 5.96% | 1.49 | 27.51% | 1.97 | 4.16% | 1.20 | -3.92 | 2.06 |
| 500 | 1.913 | 6.93% | 1.57 | 23.62% | 1.96 | 4.65% | ||||
| 5000 | 1.571 | 23.57% | 1.90 | 7.57% | 1.96 | 4.65% | ||||
| 10000 | 1.394 | 32.18% | 2.56 | 24.54% | 2.18 | 6.05% | ||||
| 0.9 | 50 | 1.448 | 6.58% | 0.81 | 47.74% | 1.48 | 4.52% | 0.72 | -4.40 | 1.55 |
| 500 | 1.413 | 8.84% | 0.87 | 43.87% | 1.48 | 4.52% | ||||
| 5000 | 1.139 | 26.52% | 1.35 | 12.90% | 1.60 | 3.22% | ||||
| 10000 | 1.062 | 31.48% | 2.05 | 32.26% | 1.91 | 23.22% |
As you can see, the measurements obtained using an oscilloscope tend to be the most accurate compared with theoretical values.
The RMS measurements are reasonably accurate when the duty cycle of the waveform is around 50% and frequency is below 1000 Hz. But when the waveform frequency increases further the measurement accuracy drops significantly. The duty cycle affects the crest factor of the the waveform, and as duty cycle drifts further from the 50% level, the accuracy also decreases.
Averaging readings are somewhat monotonic as frequency increases for a given duty cycle. The readings are hardly accurate except for a few odd-ball measurement points.
Conclusions
So from the couple of experiments conducted above, we can clearly see how signal waveform and frequency affect the accuracy of RMS measurement. In the case where the signal waveform is unknown, a digital oscilloscope tends to give the most accurate measurement.
This link on Agilent‘s website offers some more in-depth view on making accurate true RMS measurements.

