Prime number theorem dictates the asymptotic behavior of prime number distributions. In layman terms, the distance between prime numbers increases at a logarithmic pace. This gives the familiar logarithm figure.
Alternatively, if we “bin” the prime numbers according to the differences (gaps) between two consecutive prime numbers, we would yield another logarithmic distribution: the histogram of such differences will be logarithmic as well.
So, take the following sequence of prime numbers for example:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29…
The distances between the consecutive numbers in the above sequence are:
3-2 = 1
5-3 = 2
7-5 = 2
11-7 = 4
19-17 = 2
23-19 = 4
29-23 = 6
We then calculate the histogram based on the gaps.
Denote the histogram bin index as
\[i = \lfloor\frac{d}{2}\rfloor\]
For the example above, we get the following distributions for H[i]:
\[H[0] = 1, H[1] = 3 H[2]=2, H[3]=1\]
Now we calculate the distribution (H[i]) described above using prime numbers within the following interval (for all prime numbers up to 4,294,967,291):
\[[2^0, 2^{32}]\]
We can obtain the following plot for the histogram (H[i]):
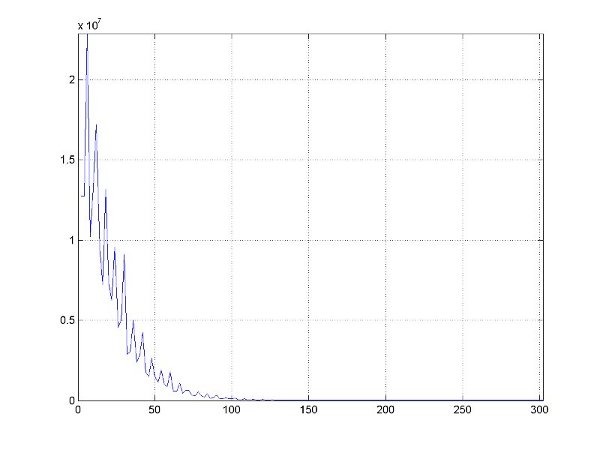
To illustrate that the distribution is indeed around a logarithm curve, we take the logrithms of the values for each H[i] and get the following figure:
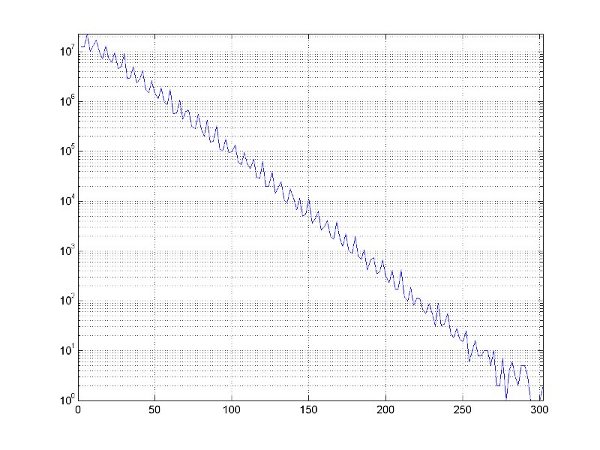
As you can see, the distribution is around a straight line.

